透视不仅是一种表现深度的方式，也是构图的一种新方法。有一种说法，中国的斜透视传自印度，后者又来源于古罗马，但是却没有确凿的证据。
早在公元1世纪或2世纪，中国东汉时期的画家已开始采用斜透视（oblique perspective）。例如，北宋时期的界画《磨坊》（局部），作者不详（传为卫贤的《闸口盘车图》），现藏上海博物馆。场景是水磨坊，周围河道环绕。这其中，斜透视与景物和人物比例的缩小相结合，达到了一定的效果。这种斜透视是画面对物体的三个方向上的主要面都倾斜的透视，多用于高层建筑物等。从某种意义上来说，接近于下面要讲述的西方绘画中的三点透视。
有一种说法，中国的斜透视传自印度，后者又来源于古罗马，但是却没有确凿的证据。事实上，除了界画《磨坊》，在清代苏州画家徐扬的画作《盛世滋生图》（又称《姑苏繁华图》，长12.25米，现藏辽宁博物馆）和日本江户时代画家乌居清长（Torii Kiyonaga,1752-1815）的浮世绘作品中，也可以见到这种技法。乌居清长的作品以色彩鲜明且和谐著称，笔下的美女被赞为“清长美人”。
▲鸟居清长的画《下棋的妇女》，约作于1780年。（本文图片来自南方周末）
据说在公元前5世纪的希腊绘画作品中，已经出现透视原理的应用。稍后，亚里士多德在《诗学》中，将透视描述为：在舞台上使用平板来提供深度的幻觉。同时代的希腊画家亚西比德（Alcobiades）也把这一技巧应用于绘画，这位画家可能是雅典将军、政治家亚西比德的后裔，后者是哲学家苏格拉底的生死之交，是典型的聪明而注重自我的雅典人，在伯罗奔尼撒战争期间，他反复于雅典、斯巴达和波斯之间而左右局势。巧合的是，欧几里得在他的光学理论中也引入了透视的数学原理。
布鲁内莱斯基
虽然有海桑这样的全才和斐波那契那样灵性的数学家，但在漫长的中世纪里，欧洲和地中海沿岸一带的数学进展缓慢，有时甚至停滞不前甚或倒退。不过，意大利的艺术家们却善于利用数学，尤其是几何学的知识和技巧，取得了世人瞩目的成就，在艺术史上留下浓重的一笔。这其中，最主要的方法有透视原理及其应用。
木刻《为躺着的妇人作画》是文艺复兴时期德国画家丢勒（Albrecht Dürer,1471-1528）的作品，它告诉我们画家是如何画出透视效果的。右边是画家本人，左边是他的模特。画家在中间放置了一块玻璃屏板，上面描好方格子，同时他的画布上也用铅笔描好方格子。模特透过玻璃屏板，会有一个轮廓呈现。例如，鼻子在点A上，膝盖在点B上，而肚脐又在点C上。画家只需依样画葫芦，便又轻松又准确地把人物描绘到平面上。
这就是透视原理（perspective principal）,但它不是丢勒的首创和发现。丢勒出生于纽伦堡，小时候在作坊里学习绘画，后来又拜名师学艺。从18岁开始，丢勒到处旅行，先是去尼德兰和瑞士，后来两次长期旅居意大利，既丰富了生活阅历，又学到了包括意大利画家的透视原理在内的绘画技巧。事实上，早在丢勒出生前半个多世纪，意大利就有一位艺术家致力于透视法的探索和实践。
大约在1413年，布鲁内莱斯基（Filippo Brunelleschi,1377-1446）展示了后来的艺术家广泛使用的透视技法的几何原理。布鲁内莱斯基出生在佛罗伦萨，他的父亲是公证人，小时候他接受父母的安排，学习文学和数学，希冀子承父业，做一名公仆。后来他依照自己的意愿改行学做金匠和雕刻师，然而由于某种原因，在一次有把握获胜的雕刻竞赛中他没有成功，一气之下又改行从事建筑设计，那时候文艺复兴运动已经开始了。
布鲁内莱斯基最重要的作品是佛罗伦萨主教堂（1420-1436），迄今它仍是包括作者在内的各国游客的必到之地，也使得他成为文艺复兴时期意大利最重要的建筑师。正是在他建筑生涯的初期，布鲁内莱斯基重新发现了原本为希腊人所知晓后来却在欧洲中世纪失传的透视原理。据说他用两块描绘佛罗伦萨街道和建筑的油画证明了他的发现，可惜这两块画板现已遗失。
从布鲁内莱斯基用来举证的两块画板上的油画是街道和建筑这件事来看，他所重新发现的透视原理很可能是没影点。所谓没影点（vanishing point），是指三维空间里两条平行的直线其延长线在视觉印象里相交于无穷远点。举例来说，铁道线的两条铁轨向无限方向延伸时，在无穷远处是相交的。这一现象并不是孤立的，又如茶杯的杯沿通常是圆形的，但看起来却像是椭圆，无论我们站在近旁还是远处。
可以说布鲁内莱斯基创立了科学绘画，他的学生和后辈中，乌切洛（Uceello,1397-1475）、德拉·弗朗切斯卡（della Francesca,1416-1492）、马萨乔(Masaccio，1401-1428？)都对透视学作出了重要贡献。马萨乔是第一个运用老师引入的透视法的画家，他的《纳税钱》比任何早期作品都更具有写实主义气息，同时表现出了距离感。16世纪的艺术史家瓦萨里（Giorgio Vasari,1511-1574）认为，马萨乔是第一个达到完全真实地描绘事物的艺术家。
从流传下来的作品来看，乌切洛并非最杰出的艺术家，他表现透视学方面的佳作随着时间的流逝被严重毁坏，已经无法复原了，不过仍然显示出景物的表面、线条和曲线的复杂性。他生前潜心于透视学这门“十分可爱的学问”之中，常常在妻子的催促下才上床睡觉。瓦萨里记载，“为了研究透视学中的没影点，他曾经通宵达旦。”
德拉·弗朗切斯卡使得透视学变得成熟，他对几何学抱有极大的热情，每个位置都事先安排得非常精确，以保持与其他图形的比例关系，同时使作品的整个部分一体化。他喜欢弯曲光滑的曲面和完整性，甚至对人物身体的每个部位及其服饰都运用了几何形式。他的作品《耶稣复活》和《鞭笞》是透视学的两幅佳作，同时也是艺术史上的珍品。
假如你有机会欣赏到古典油画，画中有家具或天花板的话，那一定是有平行线的。你将会发现，把每组相互平行的线各自朝一个方向延长，都会相交于同一点。如图所示，黄色的平行线即是延长线，它们相交于同一点，这样的家具符合透视原理，画成之后，再擦去黄线和交点，那也正是vanish这个动词的原意，即“消失”。
又如一幅名为《红色的拖车》的摄影作品，是作者在西班牙塞戈维亚乡村拍摄的。那时麦收季节已过，拖拉机开走了，只剩下拖车，天空有大片的乌云，很像一幅油画。如果仔细观察拖车的边栏，我们会发现，相互平行的上沿和下沿（均为直线）的延长线刚好相交于远处那棵无名树。值得一提的是，这组平行线并非顺着我们的视线，而是倾斜的。
阿尔贝蒂
在布鲁内莱斯基27岁那年，另一位杰出的意大利建筑师阿尔贝蒂（Leone Alberti，1404-1472）出生于热那亚，比同城出生的航海家克里斯托弗·哥伦布早了将近半个世纪。阿尔贝蒂是佛罗伦萨一位银行家的私生子，自小他就跟着父亲学习数学，后曾在帕多瓦念书，再到博洛尼亚大学深造，获得法学博士学位。之后，他随一位红衣主教游历了法国、比利时和德国，1432年定居罗马，担任教皇的秘书。
阿尔贝蒂多才多艺，他曾用拉丁文创作喜剧，在他的文艺著作《论绘画》中，首次引入了投影线和截景等概念，阐明了从三维物体到平面画布的透视原理。阿尔贝蒂也是文艺复兴时期最伟大的建筑理论家，著有十卷本的《论建筑》，此书用拉丁文写成，他认为建筑必须实用、经济、美观，尤以前两者为先决条件。在阿尔贝蒂看来，建筑物的美是客观存在的，美就是和谐和完整。
▲阿尔贝蒂的透视法。（资料图）
阿尔贝蒂还从人文主义出发，用人体的比例来解释古典柱式。他像哲学家一样提出他的思考，“一个人只要想做，他就能做成任何事情。”“我希望画家通晓全部自由艺术。但我首先希望他们精通几何学。”“借助数学的工具帮助，自然界将显得更为迷人。”不过，《论建筑》要等到阿尔贝蒂身后13年才得以出版。五个多世纪过去了，他留下的建筑仍有佛罗伦萨的鲁奇拉府邸、新玛利亚教堂，里米尼的圣弗朗西斯科教堂，曼图亚的圣安德烈亚教堂等，其风格雄伟有力。
说一说阿尔贝蒂的建筑风格。在他之前，布鲁内莱斯基继承了古希腊的遗风，通过柱子或半柱奠定了古典建筑的风范，尤以佛罗伦萨主教堂和帕齐小教堂为代表。按照20世纪英国艺术史家贡布里希爵士的说法，阿尔贝蒂创造了一种个人私宅的建筑风格，其影响一直延续至今。他选择了偏平的壁柱和檐部，像网络一样覆盖在建筑的立面。这样一来，在保留古典柱式的同时，又不改变建筑的结构，从而赋予城市邸宅以现代的形式。
说到《论建筑》，公元前1世纪的罗马建筑师马可·维特鲁威（Marcus Vitruvius）也写过十卷本的《建筑学》，书中记载了古希腊数学家阿基米德测定希罗王金王冠真假的故事。阿基米德在洗澡时发现浮力定律，同时也揭示了王冠的真假之谜。1487年前后，达·芬奇也曾画过一幅著名的素描《维特鲁威人》，那是素描的教科书中不可或缺的。画家依据《建筑学》中的描述，努力绘出最完美比例的男子人体。
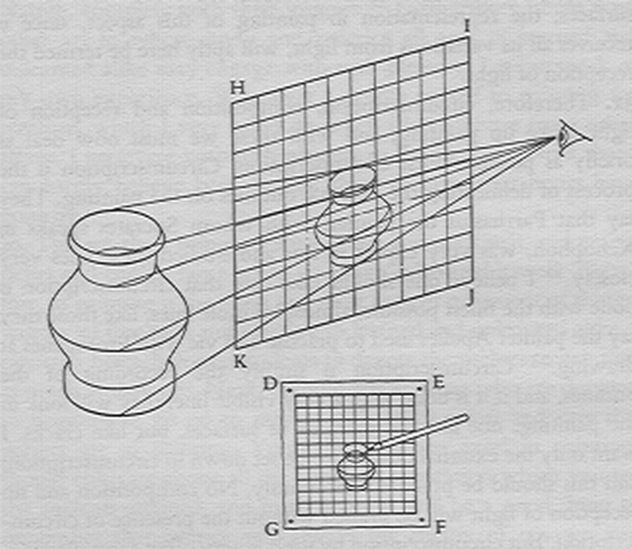
阿尔贝蒂曾宣称，一幅画就是投射线的一个截景。他画过这样一幅素描，右边是（画家的）眼睛，左边是要画一个景物，犹如杭州西湖三潭印月的三座石塔（相传是北宋大诗人苏东坡疏浚西湖时的创意，现有的石塔系明代重建）。画家在他和景物之间放置了一块画好方格子的玻璃屏板，然后模仿景物在玻璃屏板上的投影或轮廓，在同样画有方格子的画布上描绘下来。
很明显，这种利用截景的透视方法在阿尔贝蒂时代已经很流行了。难得的是，阿尔贝蒂从中提出了这样一个数学问题，假如把玻璃屏板平行移动，那么得到的截景或轮廓与原先的十分相似，他问：两者之间的数学关系是什么？这个问题比起欧几里得几何学中相似三角形的关系来，可是要复杂和困难许多，难怪那个时代全欧洲的艺术家和数学家都回答不出来。
没影点理论
透视不仅是一种表现深度的方式，也是构图的一种新方法。绘画因此开始呈现统一有序的场景，而不是多个场景的无序拼合。没影点的出现，为不同的场景的表现提供了很好的科学依据和方法。文艺复兴以来，透视法经过历代艺术家的探索，逐渐变得多种多样。透视按没影点的多少，大致可分为一点透视、二点透视、三点透视、四点透视和零点透视。
一点透视（one-point perspective）只包含一个消失在地平线的点。例如，通向远方的街道、走廊，无穷无尽延伸的铁轨，有些建筑物。这样的效果是，让画面直接面对观众。任何由与观察者的视线平行或垂直（如《红色的拖车》）的物体构成的画面都可以用一点透视来表现。其结果是，所有的平行线会在地平线的一个点（没影点）会聚。
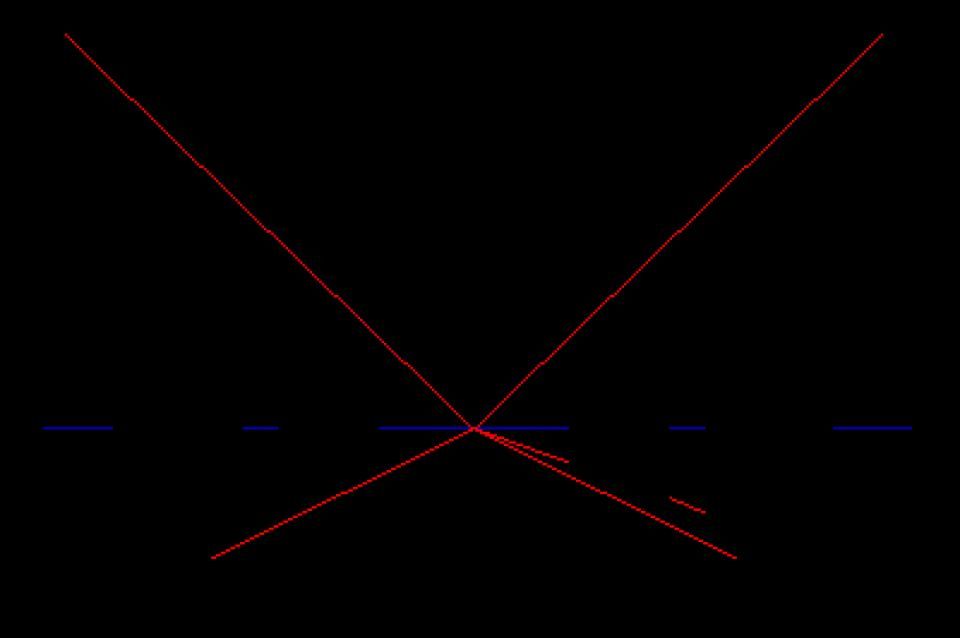▲一点透视。（资料图）
二点透视（two-point perspective）包含了两个消失在地平线上的点。例如，45度角或任何斜角呈现的建筑物，分别沿两组斜平行线延伸在远方会聚。换句话说，一个没影点代表一组平行线，另一个没影点代表另一组平行线。或者可以这么说，房子的一堵墙会向一个没影点退去，另一堵墙则向相反的一个没影点退去。
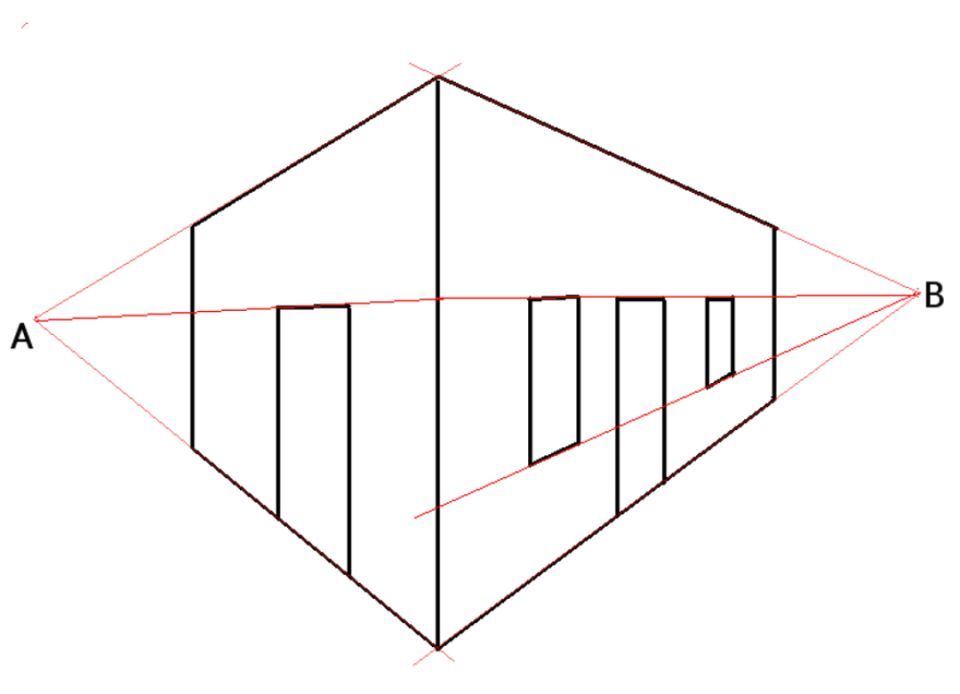▲两点透视。（资料图）
三点透视（three-point perspective）包含了三个没影点的画面。除了两个消失在地平线以外，还有一个要么消失在天空，要么消失在地下。这个取决于观察者的位置。例如，一幢高楼，会有许多垂直的平行线。如果观察者是从地面上看，那么这组平行线会会聚在天空；而如果从建筑物顶端看下去，或从附近更高的建筑物去看，那这组平行线会会聚在地面甚或地面以下。
一点、两点和三点透视取决于正在观看的场景的结构，这些透视也存在于笛卡尔坐标
系中。而四点透视（four-point perspective）是两点透视法的曲线变种，它可以是360度全景，甚至超过360度来描绘不可能的场景，这种情况可以说是虫眼（worm’s-eye）或鸟瞰图（bird’s-eye）。通过插入一组不同于三个坐标轴的任何一个的平行线，就能创建一个新的没影点，那样的话，四点透视就出现了。同样，也存在五点透视和六点透视。
没影区域（vanishing area）。有些复杂的场景需要多种没影点，那种情况下既有正面垂直的平行线组，相交于主没影点（principal vanishing point），又有两旁45度角的两组平行线，分别相交于左右的两个对角没影点（diagonal vanishing point）。进一步，主没影点和两个对角没影点三点位于同一条直线上，那条直线被称为水平线。
零点透视（zero-point perspective）,如果观察者看不到任何平行线，即看到的是非线性场景，那就是零点透视，那样的话没影点就不存在了。最典型的例子是那些自然风景，例如山脉，但它仍然是可以绘制的，虽说深度感不容易表现。另一方面，平行投影（例如仰角）是可以通过从很远的地方观看所涉及的物体来近似。那样一来，任何给定的小对象在所述场景中可因此模仿平行投影的轮廓。
而就西方人的油画来说，任何规律也都不是一成不变的。20世纪西班牙画家毕加索的立体主义作品就是把一个物体的正面反面，看得见和看不见的全都表现在一个二维的平面上，可以说他抛弃了传统的透视学，建立了自己的新规则。与毕加索同时代的法国画家马蒂斯是野兽派的代表人物，在他的一些作品里立体的轮廓消失了，垂直的墙壁与水平的桌面可以融为一体。
比毕加索稍晚的比利时画家马格利特（Rene Magritte,1898-1967）是一位超现实主义者，他的作品常常赋予我们平常熟悉的物体一种崭新的寓意，或者将不相干的事物扭结在一起，给人以一种荒诞、幽默的感觉和启示。在《欧几里得漫步处》中，右边的街道垂直于画面，越往远处两端越来越接近，最后变成了一个点，长方形变成了等腰三角形。这是没影点的应用。而左侧水塔的塔尖是个圆锥，依照初等几何学的三视图原理，圆锥的主视图和侧视图均为等腰三角形。这两个三角形几乎全等，诱发了观众的好奇心和想象力。
1987年，比利时拍摄了一部短电影《没影点》，可谓是马格利特式的幽默片。片中女教师在讲述文艺复兴时期发明的透视原理时，底下的同学们一丝不挂。随后，女教师被同学们要求脱光衣服。犹豫片刻以后，老师同意自我牺牲。结果在她脱光衣服后背身看黑板时，底下同学们迅速把衣服全部穿了起来。老师一转身大惊失色，这时候敲门声突然响起，同学们异口同声地说：come in……
中国画里的透视
所谓透视，是通过一块透明的平面去看景物的方法，然后再把这个所看到的景物准确描画在平面的画布或纸上。用线与线的位置关系，来展示物体的空间位置。大至建筑，小至日常器皿，在西方绘画中，每一幅作品，都运用了透视原理。反观中国画，并不是遵循严格的透视规律，它经常类似于多镜头分割组合的方式，比如北宋画家张择端的《清明上河图》（现藏故宫博物院），就是由无数小镜头组成。
不仅如此，中国古代画家们还采用“远大近小”的方法，这与西方绘画里的“远小近大”恰好相反。无论唐代画家阎立本的《十八学士图》（现藏台北故宫博物院），南唐画家顾闳中的《韩熙载夜宴图》，宋代苏汉臣的《妆靓仕女图》，拟或明代画家仇英的《竹院品古图》（以上三幅现藏北京故宫博物院），我们看到的桌子或茶几都是远大近小，不成比例。即便张择端的《清明上河图》，瓦片的屋顶同样也是近小远大。
▲阎立本《十八学士图》局部，现藏台北故宫博物院。（资料图）
倘若要问为什么，《芥子园画谱》给出了一种答案。在中国绘画史上，这是一部流传甚广，影响了一代又一代画家，自出版三个多世纪以来不断拓展出新，称得上是中国绘画的经典著作。在这部书的第四卷，“几席屏榻诸式”里有一段话，直接地告诉了我们，为什么在传统绘画里，器皿、家具等物体，都是以近小远大的方式进行描绘了。
书中是这么说的：“既画亭榭，安得使之空洞无物？必须几可凭可藉。画此等物，固不可太工，工则俗”。意思是，从中国古代的审美情趣来看，画家具，画席子，画屏风，画器皿，如果“太工”，像透视那样的手法来画的话，就俗了，就不雅致了，就不美了。于是，我们看到了与西方绘画透视概念完全相反的画面效果。近现代大画家如黄宾虹、齐白石、潘天寿、傅抱石等，都把《芥子园画谱》作为学习的范本。
我以为，“远大近小”或许是以画家个人为中心，向远处看的一种水波形的扩散效果，与画中的那些桌子、凳子、瓦片、床第等等，仿佛是一个个同心圆弧的合成。从某种意义上讲，这个技法也符合佛教“唯我独尊”的思维方式。当然，因为人是有两只眼睛的，水波并非由一块石头激起，因而“远大近小”的方式也各式各样。
“芥子园”是清初名士、浙江兰溪人李渔（出生在江苏如皋）在南京的别墅。他的女婿沈心友家中，藏有明代山水画家李流芳的课徒稿43幅，遂请嘉兴籍画家王概整理增编90幅，增至133幅，并附临摹古人各式山水画40幅，为初学者作楷范。因得李渔资助，于康熙十八年（1680）套版精刻成书，即以“芥子园”名义出版。此乃《芥子园画谱》第一集。
之后，王概又受沈心友之托，与他的胞兄王蓍、胞弟王臬一起，共同编绘了“兰竹梅菊”与“花卉翎毛”谱，于是有了《芥子园画谱》第二集和第三集。那是在康熙四十年（1701），用开化纸木刻五色套版印成，世称“王概本”。在当时印刷质量较为精致，但印数很少，只印了几百部。
《芥子园画谱》后来一再翻版，到光绪年间，已磨损得不能再印。于是，有一个叫巢勋的画家，也是嘉兴人，临摹了前三集，并增编一批上海名家画作，同时又编绘了一干人物，此即第四集。全部四集于1897年由上海有正书局以石印法影印出版，世称“巢勋本”。这套《芥子园画谱》虽是黑白版本，但比“康熙版”丰富许多。对上述问题的解答，正是出自“巢勋本”第四集。（完）
作者/蔡天新
